映像图分析计算
使用手册
[TOC]
简介
映像图分析是对原始数据的一个初始的、直观的分析处理。类比成人,可以算是一种”面相“、”第一印象“,所反映的,就是这个时刻的所考虑的设备参数的直观展示。
所谓的映像分析,就是一个把这些参数都综合起来,变成一个直观的画面,让这个画面能呈现出 “满脸红光”,“气色不错”,或者 “脸色不好” 的特征,让我们一看就知道大概是怎么回事。除此以外,我们不仅要看到静态的,还要看到这个画面发⽣的变化。
基本概念
一台⼯业设备(物联⽹对象),动辄上百个参数变量,时时刻刻这些参数的数据都在变化。这么多参数,我们应该看哪一个?又能看出来什么名堂?答案是看不出什么。因为⼯业设备的机理已经是⾮常复杂,各个参数之间的相互关系也⾮常复杂,即便去看每一个参数,也很难弄明⽩这个设备整体到底是什么个状况。
在这种情况下,我们引入了雷达图这个利器来帮助我们分析。雷达图的构造就一系列的同心圆构成,并有八个方向的轴线。每一个同心圆实际上就是这些轴线的刻度,这样我们可以同时表示出八个数据。我们用一个绿色的同心圆,表示这八个数据分别的均值;两个红色的同心圆分别表示Upper Threshold(上阈值)和Lower Threshold(下阈值)。
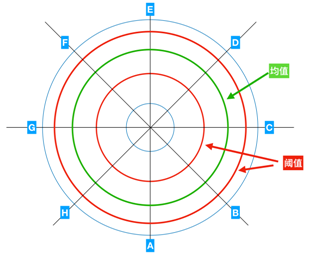
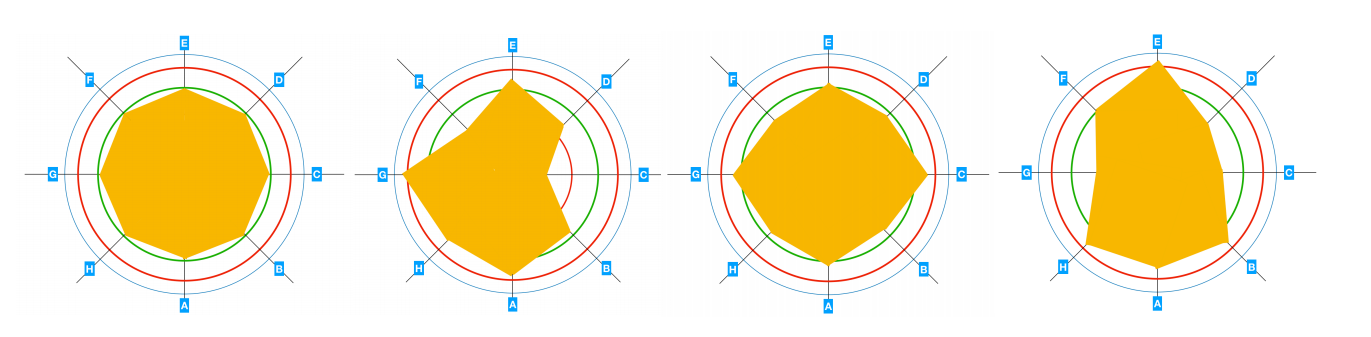
我们把每次采样的八个参数对应在ABCDEFFGH八个轴对应的刻度上,把他们连起来,染成颜色(黄色)后观察。
数据标准
假设,一个对象有 9 个 FV 变量,我们就⽤ X1,X2,X3,…,X9 来代表。我们这样来想,对象是在运转的,因为机器设备在运转。对象如果不是在运转,我们认为这个对象是静⽌的,静⽌的数据对我们也没有任何意义,只有在运转的时候,对象的数据才有意义。那么,我们闭着眼睛来想象一下,把这个运转的对象想象成一个行⾛在路上的车轮,把所有的 FV 想象成这个车轮的 “轮胎”,参数均匀布满了这个轮胎,而 FV 的值就相当于这个 FV 位置的轮胎厚度。
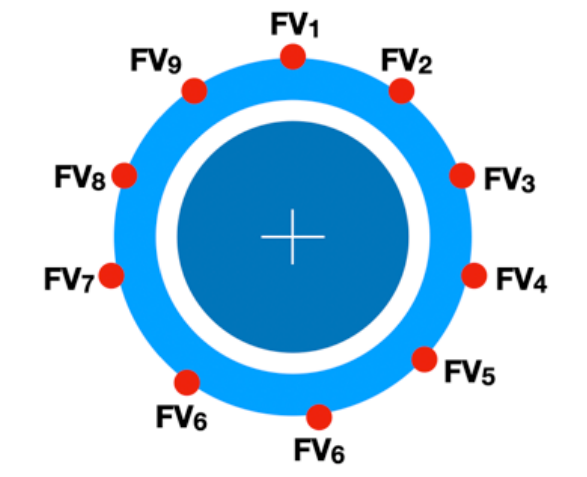
数据标准化,就是我们事先要对这些 FV 先做一个处理,把他们的数值都变形到差不多的比例,这样,这个在一开始的时候,跟我们的汽车轮胎一样,厚薄均匀。
这是因为 FV 实际的数值,有些可能在 1000 ~ 6000 之间波动,有些在 300 ~500 之间波动,而有些可能在 0.01 ~ 0.19 之间波动,如果我们原封不动把这些数字作为这个轮胎的厚度,那这个轮胎天⽣就是个问题轮胎。
这个就是一个拉伸,把原始数据始终 ÷100,× 100, ÷ 10,大概就是这个意思。我们假设这些数据可以这样做,是因为这些数据之间都是独⽴的,这是一个合理的拉伸。
我们拿前六个参数举个例子, 我们先看这六个参数一段时间的数据片段:
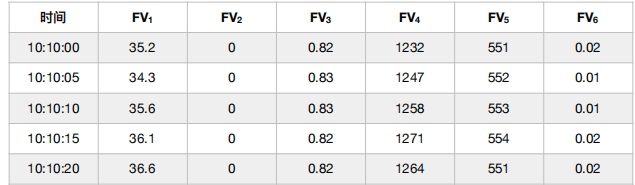
然而,我们如果要衡量⼀个 FV 对⼀个对象的 “影响力”,就不能光从这些数值来看了,有些变化个 0.1 就不得了,有些变化个好几百也没啥大碍。所以,Indass 还有两个⾮常重要的概念,⼀个叫 Scale(拉伸比例),⼀个叫 Weight(权重)。
比例的意思是,不管你的物理含义是啥,我们先找⼀条基准线(比如是 100),直接把你这个数值都放大或缩小再说。这样,每个 FV 都有⼀个⾃⼰相对确定的 Scale 值(S1 ~ S6),再重新把数值计算⼀下(SFV1 ~ SFV6),那之前的这些时序数值就变成:

那这些值,至少是在⼀个水平面上了,所以,Scale 值的作⽤,是让这些数值本身都差不多,大家起点差不多⼀样,才好有后面的说法。
Scale 是⼀个客观值,我们看到⼀个 FV 的数值,把它对应的 Scale 值找到,就知道原始的数值应该是多少。
但是,光有 Scale 并不足以评价这些 FV 对这个对象的 “影响力”,所以,除了 Scale 这个 “客观值”外,还需要⼀个 “主观值”,这个就是我们说的 Weight,权重值。权重值是我们赋予它的,不管这个权重是怎么确定的,按什么标准确定的,但都是我们给它的,所以颇有 “主观” 的意味。
Weight(权重值)的定义是这样的,6 个 FV(FV1 ~ FV6),每个都配有⼀个权重(W1 ~ W6),并让 所有的权重值加起来为1,而且权重值的相对大小,就是该参数(FV)对这个对象的 “影响力” 的大小。
要注意的是两点:⼀个是权重值是某⼀组 FV 而⾔的,他们的大小是相对的;另⼀个是,⼀组 FV 的权重值,是相对某个确定的对象而⾔的。这里面都是只有相对的概念,而没有绝对的概念。比如,“电流” 这个含义的值,对某个对象可能是至关重要的变量,而对另⼀个对象却⽆关紧要。
我们把 Scale 和 Weight 都提上去,重新组织⼀下表格,这个就看得清楚了:

界面说明
映像图分析计算一共有3个界面,接下来我们分别展示:
项目管理
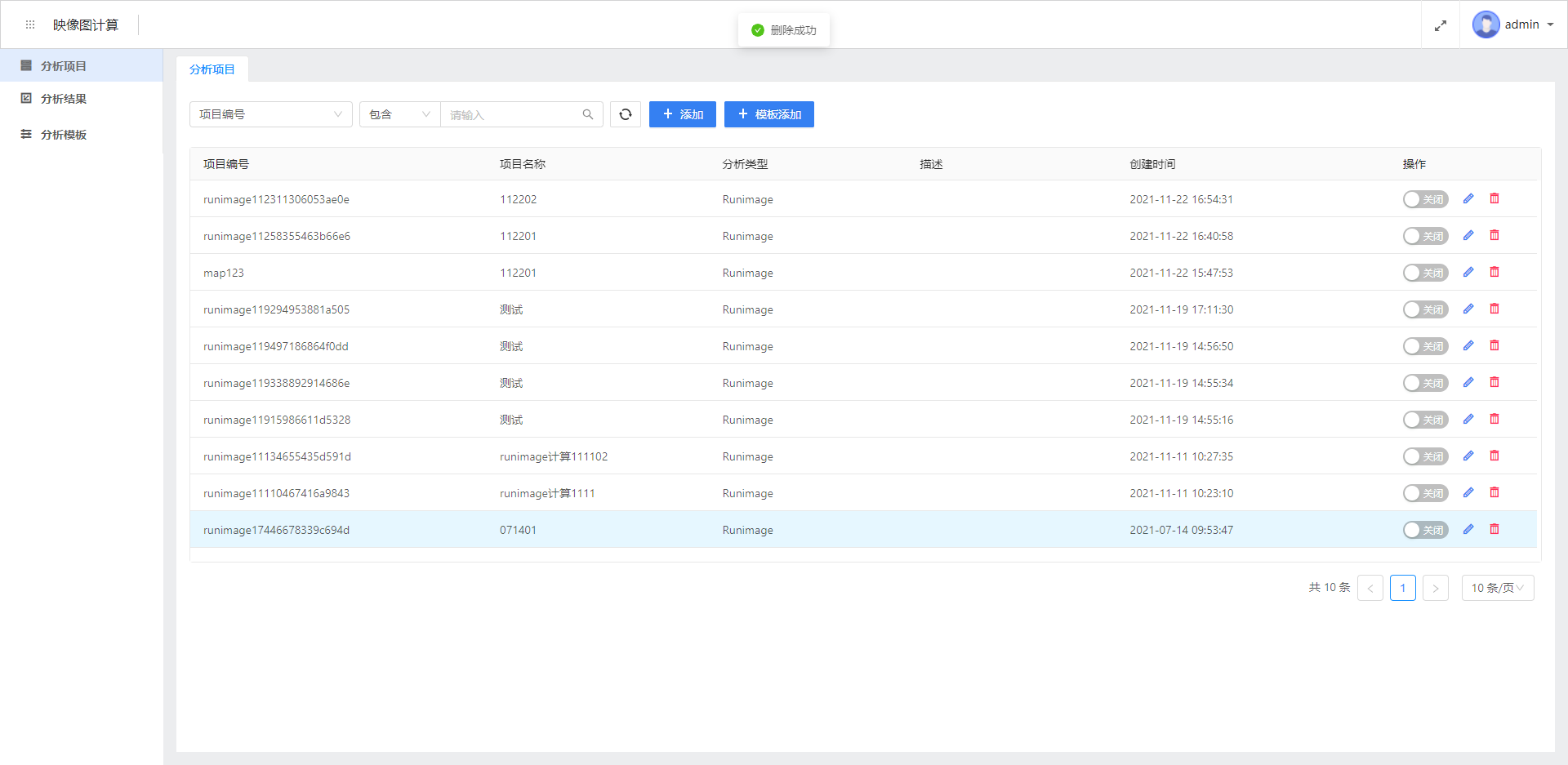
项目管理界面,可以在这个界面进行增删改查的管理,同时还可以管理项目的启停。可以点击添加按钮添加项目,也可以点击某一个项目名称,编辑这个项目的详细问题。
具体怎么配置、修改一个项目,将在下文详细介绍,这里不再赘述。
本界面还有分析对象,描述的是这个项目绑定下的所有对象,结果列表,描述的是本项目下的所有计算结果。
分析模板
 本界面可以查看、编辑映像图分析的分析模板,模板用于快速创建项目。
本界面可以查看、编辑映像图分析的分析模板,模板用于快速创建项目。
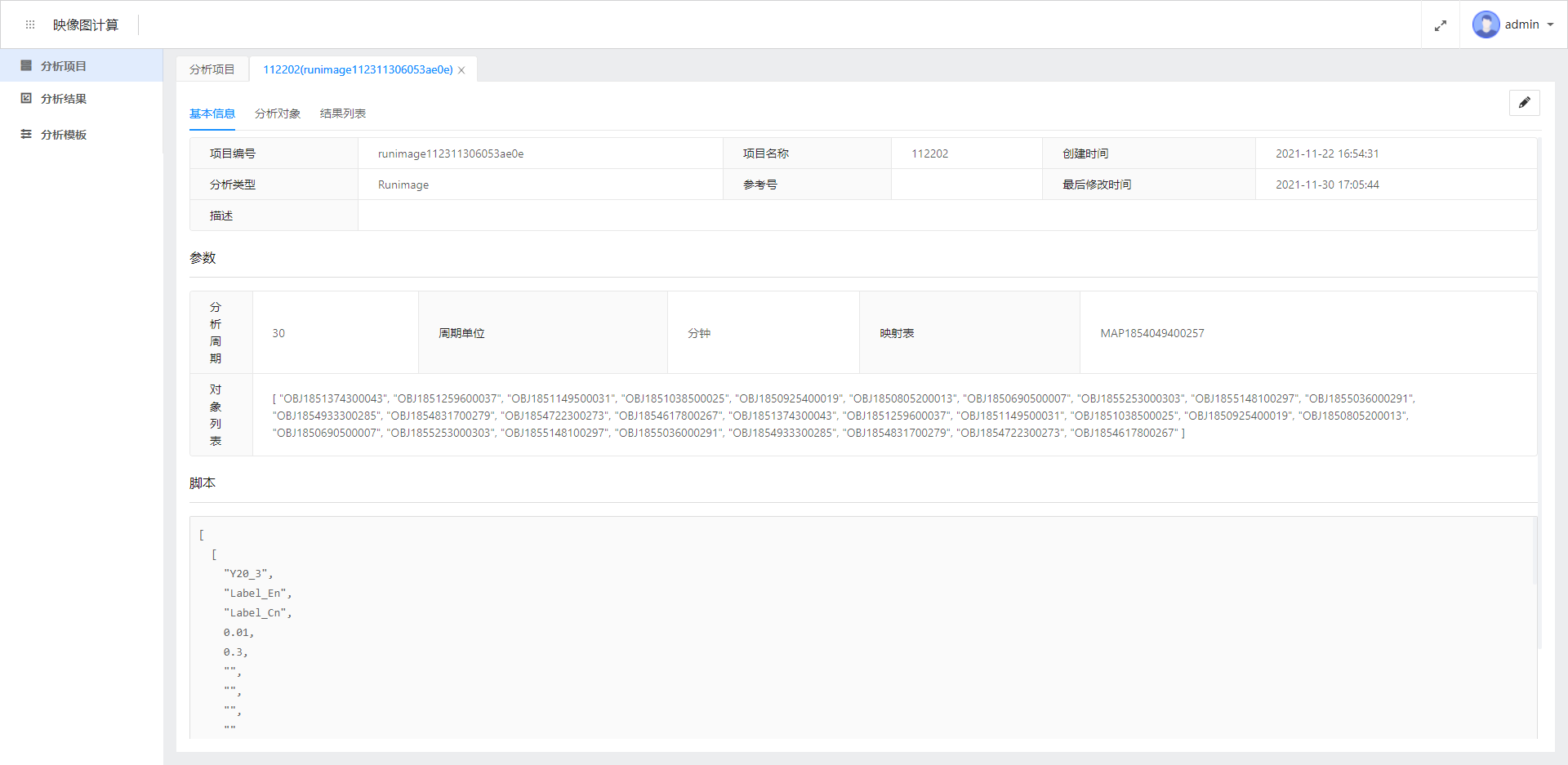
项目配置

- 项目名称:项目名称要求不能重复,其具体名称可以从实际需要和便利性出发,填写项目名称。
- class名称:根据需要选择class名称,目前映像图分析有以下class:
| class中文名 | Class英文名 | 具体功能 |
|---|---|---|
| 映像图分析计算 | Runimage | 对所选参数的标量化处理 |
- 分析计算周期:可选项有:
分钟、小时、其他等等,其他的含义为秒,可以根据需要自行填写,填写范围是从0-999。 - 限定映射表:此处可以关联MixIOT中所有已有的映射表,如果选择
限定映射表,根据要分析的对象,在映射表标识选择相应的映射表。如果选择不限定映射表,那么在对象ID中,直接选择对象。 - 分析计算对象:分析对象有
限定和不限定两个选项。如果选择限定对象,可以接下来选择对象,表示计算这个映射表项目下的一个或者几个对象。如果选择不限定对象,那么就会针对这个映射表,每次计算都动态获取映射表下的所有对象,并分析每个对象下的选定数据。
脚本规范
二维Json数组
首先,脚本必须为Json格式,否则无法创建项目。每一行为一个分析变量,可以同时存在多行。格式如下:
[
["FV", "Label_En", "Label_Cn", "Weight", "Scale", "Normal", "Tag", "Qmin", "Qmax"]
]
脚本示例如下:
[
["S01", "Label_En", "Label_Cn", 1, 0.3, "", "", -5, 5],
["S02", "Label_En", "Label_Cn", 1, 0.3, "", "", -5, 5],
["S03", "Label_En", "Label_Cn", 1, 0.3, "", "", -5, 5],
["S13", "Label_En", "Label_Cn", 1, 0.2, "", "", -5, 5],
["S14", "Label_En", "Label_Cn", 1, 0.2, "", "", -5, 5],
["S15", "Label_En", "Label_Cn", 1, 0.2, "", "", -5, 5],
["S77", "Label_En", "Label_Cn", 1, 0.14, "","", -5, 5],
["S78", "Label_En", "Label_Cn", 1, 0.1, "", "", -5, 5]
]
填写要求
一行有9个字段,在算法计算的时候使用。
| 字段 | 含义 | 备注 |
|---|---|---|
| FV | 分析参数标识 | 对应映射表的参数 |
| Label_En | 英文标签 | 变量英文描述说明,可填"" |
| Label_Cn | 中文标签 | 变量中文描述说明,可填"" |
| Weight | 参数权重 | 填写本参数的重要性占比权重 |
| Scale | 参数比例 | 填写本参数的数值大小缩放比例 |
| Normal | 参数标准值 | 本block不需要,可填"" |
| Tag | 参数标签 | 本block不需要,可填"" |
| Qmin | 参数最小值 | 本block不需要,可填"" |
| Qmax | 参数最大值 | 本block不需要,可填"" |
脚本中必填的列是:FV、Weight、Scale,并且Weight和Scale必须是数字,Tag可填可不填,填写的话将会起到过滤的作用,保留所有等于该值的数据,其余项用""填空,下面我们逐一介绍。
FV对应的就是对象参数。对象,就是MIXIOT系统中相对应的设备。在建立对象的时候,还要绑定相应的映射表,这里的FV,就对应着相应映射表中的参数。按照我们上文说明的规则选择、填写脚本中第一列的FV,选择了多少个FV,本脚本就有多少行。
Weight,就是上文提到的参数权重,填写的原则就是,谁更重要填写的权重就更大,谁不重要填写的就偏小,建议权重的填写范围在0~1之间。对于权重的填写,其实是没有标准答案的,第一次填写,可以先暂定一个值,计算出结果以后,有必要再进行调试。
Scale,就是参数比例。在实际设备数据中,有可能某些参数范围在0~1之间,比如说压力,有些参数范围是在0~1200,比如说用电量,他们的数据相对大小非常大。假如压力从0上升到1,已经是非常大的变化,但是对于转数,从999到1000,实际上是一个非常平稳的正常波动。
基于这种数据量纲的问题,我们就使用Scale来规避这种问题,对参数数据进行缩放。假如我们想把上面的两个参数缩放到10,那在压力参数的Scale中填写10÷1=10,在转速参数的Scale中填写10÷1000=0.01。经过缩放,两个参数的范围都规整到了0~10中。
Tag,本分析项目中不需要
Qmin,本分析项目中不需要
Qmax,本分析项目中不需要
应用实例
现在,我们让这个车轮转动,意思是 FV 的数据来了,这个车轮贴在地面行走,我们把这个车轮中心的轨迹记录下来,这个时候,这个车轮中心的轨迹就是一条清晰⽆比的曲线。
如果再运行中,FV 没有什么变化,或者变化的幅度很小,那么,我们会看到的轨迹是这样的:
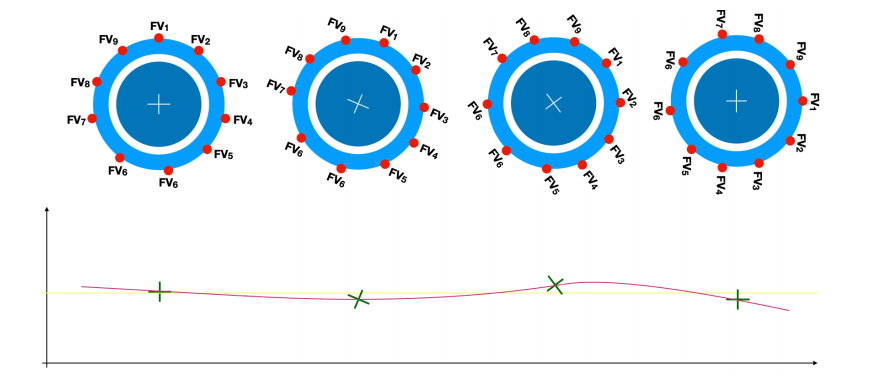
我们可以看到,这条轨迹基本上是平的,算波澜不惊。如果我们想象,⾃⼰正坐在这个⽤ FV 做车轮的对象的车子上,感觉到的是什么?平稳,舒适。
如果在运行中,FV 的变化还比较大,我们可能看到的是这样的:
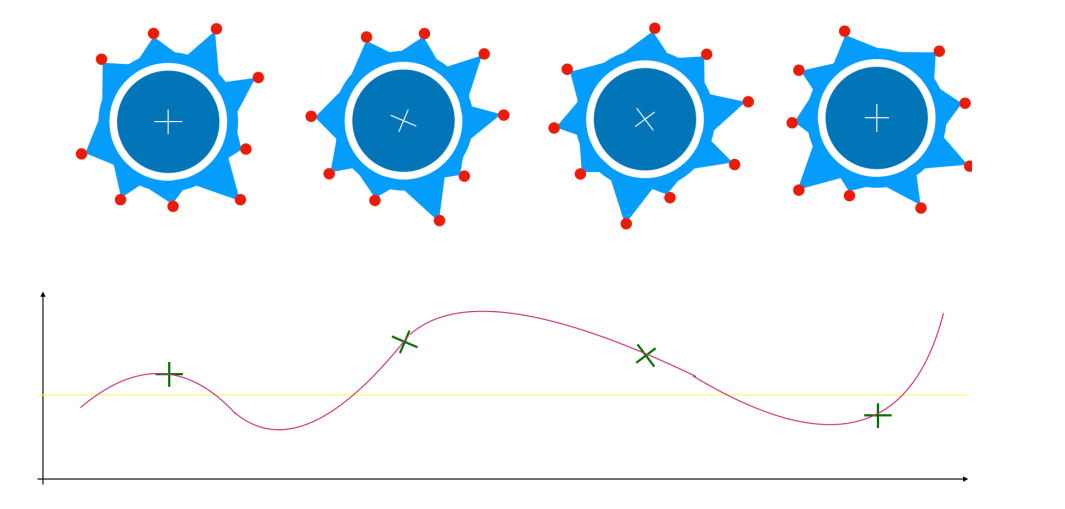
那这个轨迹的曲线,跟前面的曲线相比,很显然就算得上波澜起伏了,我们感觉到的比会是什么?颠簸,甚至是惊悚。
既然 FV 是对象在地上转动的轮子,那我们就应该了解,这个轮子三百六十度一圈,只有部分地方是跟地面接触的,如果 FV 不密集的话,可能一两个点跟地面接触,如果 FV 密集一些,那就会多一些 FV 点跟地面接触,而中心点的轨迹(高低)只跟这些跟地面接触的点有关系,而跟别的点没有关系。但是要注意,在不同的时刻,跟地面接触的点是不一样的,因为车轮在转动。
那么,是不是只要 FV 变化,我们的感觉一定是颠簸惊悚呢?其实未必,如果某个 FV 增加的时候,其他的 FV 也跟着增加;FV 减少的时候,其他的 FV 也跟着减少,而且这个 “跟着” 还能跟得上滚滚车轮的节奏,那么,我们虽然有感忽高忽低,但是不至于颠簸惊悚。如果我们把这些 FV 在增加(或减少)的幅度都按比例缩水或放水,那基本上还是平稳的。
我们现在来捋一捋,9 个不相干的,不能相互换算的 FV,本是 9 个不同的因素,我们列不出个方程,也求不出个解,但整到一起竟然变成了一条曲线。这条曲线,跟这 9 个 FV 既有关系,又没关系。而且,即便是有关系,这个关系随着时间的改变也会改变。